2012年岩土工程师考试基础知识模拟试题:高等数学(单项选择题2)
发布时间:2012-07-25 共1页
高等数学(单项选择题2)
| 一、单项题的备选项中只有一个最符合题意,错选、多选均不得分。 |
1.设f(x)是奇函数,且F(x)=f(x)·[1/(a.gif) +1)-1/2]。其中a为不等于1的正常数,则函数F(x)是: +1)-1/2]。其中a为不等于1的正常数,则函数F(x)是: |
| 正确答案:B 解题思路:这是一道概念题,应用奇函数、偶函数的定义,通过代数变形导出最后的结果。 F(-x)=f(-x)[1/(a  +1)-1/2]=-f(x){1/[(1+a +1)-1/2]=-f(x){1/[(1+a.gif) )/a )/a.gif) ]-1/2}=-f(x)[a ]-1/2}=-f(x)[a.gif) /(1+a /(1+a.gif) )-1/2] )-1/2]=-f(x)[2a .gif) -(1+a -(1+a.gif) )]/2(1+a )]/2(1+a.gif) )=-f(x)(a )=-f(x)(a.gif) -1)/2(1+a -1)/2(1+a.gif) ) )=-f(x)(a .gif) +1-2)/2(1+a +1-2)/2(1+a.gif) )=-f(x)[1/2-1/(1+a )=-f(x)[1/2-1/(1+a.gif) )] )]=f(x)[1/(1+a  )-1/2]=F(x) )-1/2]=F(x)F(x)是偶函数。 |
|
|
2.已知幂级数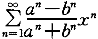 (0<a<b),则所得级数的收敛半径R等于: (0<a<b),则所得级数的收敛半径R等于: |
正确答案:D 解题思路:本题考查幂级数收敛半径的求法。可通过连续两项系数比的极限得到ρ值,由R=1/ρ得到收敛半径。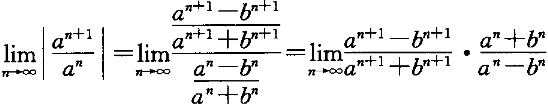 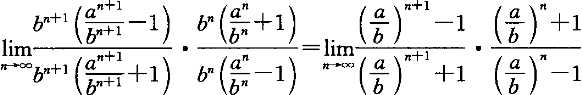 =(-1)/(-1)=1=ρ R=1/ρ=1 |
|
|
3.设二重积分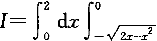 f(x,y)dy,交换积分次序后,则I等于: f(x,y)dy,交换积分次序后,则I等于: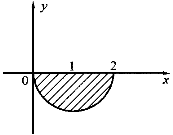 |
| 正确答案:A 解题思路:本题考查二重积分交换积分次序方面的知识。解这类题的基本步骤:首先根据原积分次序画出积分区域的图形,得到阴影部分的图形;然后写出先x后y的积分表达式。 由 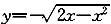 ,y ,y.gif) =2x-x =2x-x.gif) ,x ,x.gif) -2x+y -2x+y.gif) =0,(x-1) =0,(x-1).gif) +y +y.gif) =1。 =1。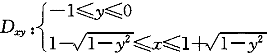 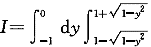 f(x,y)dx f(x,y)dx |
|
|
| 4.下列函数在所给区间中,满足罗尔定理条件的是: |
| 正确答案:D 解题思路:本题属于概念题,根据满足罗尔定理的三个条件(在闭区间连续,在开区间可导,两端函数值相等)来判定。 A.f(x)=x .gif) 在[0,3]两端函数值不相等。 在[0,3]两端函数值不相等。B.f(x)=1/x,f′(x)=-1/x .gif) 在(-1,1)可导的条件不成立,在x=0不可导。 在(-1,1)可导的条件不成立,在x=0不可导。C.f(x)=|x|在x=0处的导数,用左右导数定义计算, 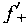 (0)=1, (0)=1,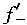 (0)=-1,因而在x=0处不可导,从而在(-1,1)内可导不成立。本题的结论应记住。 (0)=-1,因而在x=0处不可导,从而在(-1,1)内可导不成立。本题的结论应记住。D.f(x)=x  在[0,3]上连续,f′(x)= 在[0,3]上连续,f′(x)=.gif) -x/2 -x/2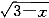 在(0,3)上可导,f(0)=f(3),满足罗尔定理。 在(0,3)上可导,f(0)=f(3),满足罗尔定理。 |
|
|
5.求 xf(x xf(x.gif) )·f′(x )·f′(x.gif) )dx等于: )dx等于: |
正确答案:D 解题思路:本题为抽象函数的不定积分。考查不定积分凑微分方法的应用及是否会用不定积分的性质 f′(x)dx=f(x)+c。 f′(x)dx=f(x)+c。 xf(x xf(x.gif) )f′(x )f′(x.gif) )dx= )dx= f′(x f′(x.gif) )f(x )f(x.gif) )d(1/2)x )d(1/2)x.gif) =(1/2) .gif) f′(x f′(x.gif) )?f(x )?f(x.gif) )dx )dx.gif) =(1/2) =(1/2) 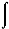 f(x f(x.gif) )df(x )df(x.gif) ) )=(1/2)·(1/2)[f(x .gif) )] )].gif) =(1/4)[f(x =(1/4)[f(x.gif) )] )].gif) +c +c |
- 2012年岩土工程师考试基础知识模拟试题:工程地质(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:理论力学(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:高等数学(单项选择题3)
- 2012年岩土工程师考试专业知识考前冲刺(五)上午卷
- 2016年岩土工程师考试《综合知识》冲刺练习(4)
- 2012年岩土工程师考试基础知识模拟试题:弹性力学和结构力学(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(3)
- 2012年岩土工程师考试基础知识模拟试题:电工与电子技术(单项选择题2)
- 土工结构、边坡与支挡结构、基坑与地下工程(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(5)

