2012年岩土工程师考试基础知识模拟试题:理论力学(单项选择题1)
发布时间:2012-07-25 共1页
理论力学(单项选择题1)
| 一、单项题的备选项中只有一个最符合题意,错选、多选均不得分。 |
1.图4-5(a)所示机构由两曲柄O A和O A和O B,半圆形平板ACB及铅直杆CD组成,它们都在图示平面内运动。已知曲柄O B,半圆形平板ACB及铅直杆CD组成,它们都在图示平面内运动。已知曲柄O A以匀角速度ω= A以匀角速度ω= rad/s绕轴O rad/s绕轴O 朝逆时针方向转动,O 朝逆时针方向转动,O A=O A=O B=15cm,O B=15cm,O O O =AB,半圆形平板的半径r= =AB,半圆形平板的半径r=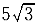 cm,O cm,O 和O 和O 位于同一水平线上。则在图示位置时,CD杆的加速度a 位于同一水平线上。则在图示位置时,CD杆的加速度a 为( )。 为( )。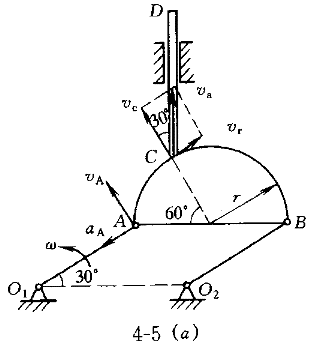 |
正确答案:B 解题思路:解:由于O A=O A=O B,O B,O O O.gif) =AB,故半圆形平板ACB作平动。取CD杆上的C点为动点,动系与半圆形平板固连(平动系)。于是 =AB,故半圆形平板ACB作平动。取CD杆上的C点为动点,动系与半圆形平板固连(平动系)。于是v  =v =v a  =a =a A点的速度和加速度大小分别为 v  =OA·ω=15· =OA·ω=15· =15 =15.gif) cm/s cm/sa  =OA·ω =OA·ω =15·( =15·(.gif) ) ) =15 =15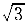 cm/s cm/s 它们的方向如图5所示。 根据已知条件和速度合成定理,作出动点的速度平行四边形如图5(a)所示,从而可得: v  =v =v etan30°=v etan30°=v Atan30° Atan30°= 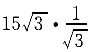 =15cm/s =15cm/s标出动点C的各项加速度如图4-5(b)所示,并选图示坐标系czy。 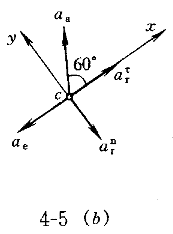 根据牵连运动为平动时点的加速度合成定理,此时有: 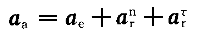 将此矢量式向图示y轴投影,得: 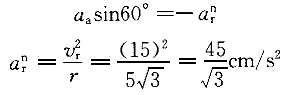 于是 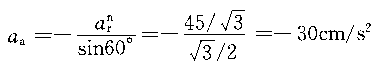 a  为负值,说明a 为负值,说明a 在图上所设指向与实际情况相反,即a 在图上所设指向与实际情况相反,即a 的方向铅直向下。所得a 的方向铅直向下。所得a 即为此时CD杆的加速度a 即为此时CD杆的加速度a 。 。故应选择B。 |
|
|
2.图4所示机构中,曲柄OB朝逆时针向转动,并带动杆AC,该杆上点A和滑块在水平滑槽内运动。已知:AB=OB=20cm;BC=40cm,曲柄OB与铅直线的夹角φ=4t(t以秒计),则当φ=π/2时,AC杆上C点的速度大小v 为( )。 为( )。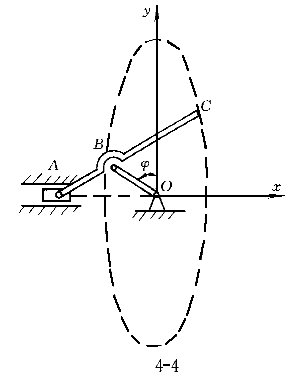 |
| 正确答案:D 解题思路:解:取图示直角坐标系Oxy,由题意知,在任意瞬时t,曲柄OB与y轴的夹角ψ=4t,且△ABO是等腰三角形,∠BAO=∠BOA=π/ψ。于是,由几何关系可得C点的运动方程为: x=ACcos(π/ψ)-(AB+OB)cos(π/ψ) =(20+40)sinψ-(20+20)sinψ =20sinψ==20sin4t y=ACsin(π/ψ)=(20+40)cosψ =60cosψ==60cos4t从而可得 v  = =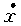 =20·4cos4t=80cos4t =20·4cos4t=80cos4tv  = =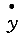 =60·4sin4t=-240sin4t =60·4sin4t=-240sin4t当ψ=4t=π/2时,有 v 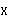 =0 =0v 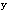 =-240cm/s =-240cm/s所以,此时C点的速度大小为 v= 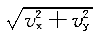 =240cm/s =240cm/s故应选择D。 |
|
|
3.图9所示一重量为W、半径为r的均质圆柱,沿一半径为R的圆柱面上作纯滚动,圆柱体在圆柱面最低点A附近作微小振动时的固有圆频率p为( )。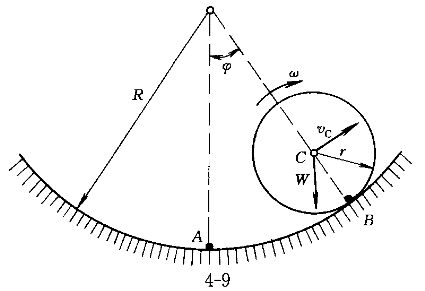 |
正确答案:B 解题思路:解:取ψ为广义坐标,以静平衡位置为势能的零位置。因重力为有势力,圆柱滚而不滑时约束力不作功,所以可用机械能守恒定理建立运动微分方程。由vc=(R-r) 和vc=rω 和vc=rω可知ω=R-r  /r /r其动能为 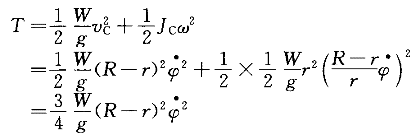 势能为V=W[R-r-(R-r)cosψ] 由机械能守恒定理T+V=const,有  +W[R-r-(R-r)cosψ]=const +W[R-r-(R-r)cosψ]=const将上式两边对t求导,再消去公因子 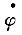 得 得 +W(R-r)Sinψ=0 +W(R-r)Sinψ=0当ψ微小时,sin≈ψ,得  +2gψ/3(R-r)=0 +2gψ/3(R-r)=0从而得知p=  故应选择B。 |
|
|
4.图7所示OA杆绕O轴朝逆时针向转动,均质圆盘沿OA杆滚动而无滑动。已知圆盘的质量m=20kg,半径R=10cm。在图示位置时,OA杆的倾角为30°,其转动的角速度ω.gif) =1rad/s,圆盘相对OA杆转动的角速度ω =1rad/s,圆盘相对OA杆转动的角速度ω.gif) =4rad/s,OB= =4rad/s,OB= cm,则此时圆盘的动量大小为( )。 cm,则此时圆盘的动量大小为( )。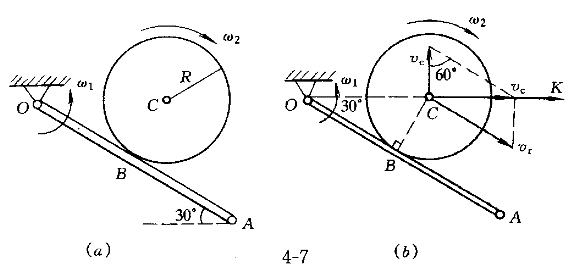 |
| 正确答案:D 解题思路:解:先用点的合成运动的方法求圆盘质心C的绝对速度vC。取C点为动点,动系选为与OA杆固连的转动系,根据已知条件和速度合成定理,作出动点C的速度平行四边形如图7(b)。而 v[e.gf]=OC·ω .gif) =R/sin30°·ω =R/sin30°·ω.gif) =10/0.5×1=20cm/s =10/0.5×1=20cm/sv 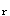 =R·ω =R·ω.gif) =10×4=40cm/s =10×4=40cm/s从而得知v  ⊥v ⊥v.gif) ,于是有 ,于是有v  =v =v tan60°= tan60°= cm/s cm/s所以,圆盘的动量大小为 K=mv  =20· =20·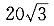 = =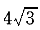 N·s N·sK的方向水平向右。 故应选择D。 |
|
|
5.一绳索跨过均质定滑轮B,绳的一端挂一重物A;另一端缠绕一均质圆柱C,如图8(a)所示。已知重物A的质量为mA;定滑轮B和圆柱C的质量分别为mB和mc,它们的半径均为r。绳的质量略去不计,它对定滑轮无相对滑动。设m =m =m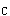 =2m =2m ,则定滑轮与圆柱之间绳索的拉力T为( )。 ,则定滑轮与圆柱之间绳索的拉力T为( )。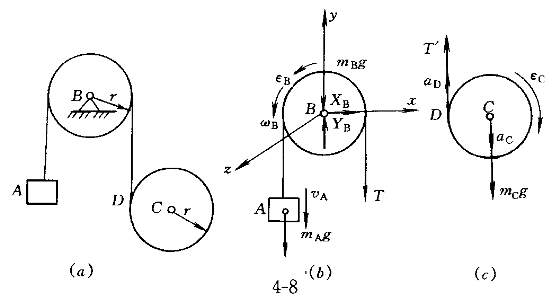 |
正确答案:A 解题思路:解:以定滑轮B连同重物A为研究对象,其受力图和所取直角坐标系Bxyz如图8(6)所示。由动量矩定量dH /dt=Em /dt=Em (F (F )有 )有d/dt(1/2mBr  ·ωB+mAvA·r)=mAg·r-T·r ·ωB+mAvA·r)=mAg·r-T·r将m  =2mA和v =2mA和v =rωB.gif]代入,并注意到dω =rωB.gif]代入,并注意到dω /dt=ε /dt=ε 有 有2m  r r.gif) ε ε =m =m gr-Tr即T=m gr-Tr即T=m g-2m g-2m rε rε (1) (1)再取圆柱C为研究对象,其受力图如图8(c)。由刚体平面运动微分方程有 mcac=mcg-T′ 1/2mcr .gif) ·εc=T′·r ·εc=T′·r将mc=2m  、T′=T和ac=rεc=ad=rεc-rε 、T′=T和ac=rεc=ad=rεc-rε 代入,有 代入,有2m  ·r(εc-ε ·r(εc-ε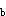 )=2m )=2m g-T(2)m g-T(2)m.gif) r r.gif) εc=Tr(3) εc=Tr(3)由式(1)~式(3)三式联立解得 T=3/4m 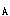 g g故应选择A。 |
- 2012年岩土工程师考试基础知识模拟试题:工程地质(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:理论力学(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:高等数学(单项选择题3)
- 2012年岩土工程师考试专业知识考前冲刺(五)上午卷
- 2016年岩土工程师考试《综合知识》冲刺练习(4)
- 2012年岩土工程师考试基础知识模拟试题:弹性力学和结构力学(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(3)
- 2012年岩土工程师考试基础知识模拟试题:电工与电子技术(单项选择题2)
- 土工结构、边坡与支挡结构、基坑与地下工程(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(5)

