2012年岩土工程师考试基础知识模拟试题:材料力学(单项选择题1)
发布时间:2012-07-25 共1页
材料力学(单项选择题1)
| 一、单项题的备选项中只有一个最符合题意,错选、多选均不得分。 |
1.某简易起重设备的吊车大梁如图6(a)所示。梁AB由20a工字钢制成,在中间一段的上下两面焊上长度为2.2m,宽度为120mm,厚度为10mm的钢板。已知材料的许用应力[σ]=152MPa,[t]=95MPa。荷载P在全梁移动,则梁的容许荷载[P]为( )。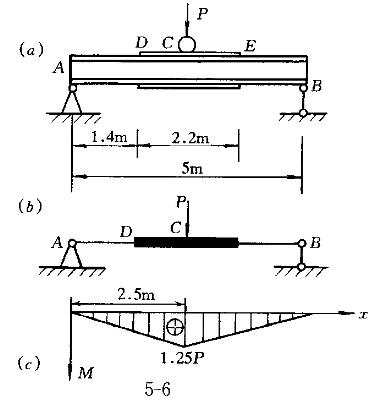 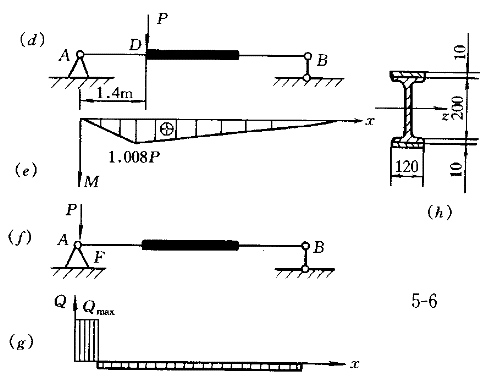 |
正确答案:A 解题思路:这在弯曲应力和弯曲强度中是一个综合性较强、影响因素较复杂的一个题。既要考虑正应力强度,又要考虑剪应力强度,同时还要考虑荷载移动时可能产生的几种最不利情况。现分析如下:由于荷载是移动的,有三种最不利的荷载位置:考虑正应力强度时,当荷载作用在跨中C点时(图6b),该截面的弯矩是全梁的绝对最大弯矩;当荷载P作用在D(或E)点时(图6a),该截面的弯矩M (或M (或M )是荷载在移动过程中该截面弯矩的最大值,也是未加强段截面弯矩的最大值。考虑剪应力强度时,当荷载P紧靠支座A(或B)时(图6f),靠近支座的截面的剪力最大。 )是荷载在移动过程中该截面弯矩的最大值,也是未加强段截面弯矩的最大值。考虑剪应力强度时,当荷载P紧靠支座A(或B)时(图6f),靠近支座的截面的剪力最大。1.荷载作用在跨中C点时,由C截面的正应力强度求[P]。 当荷载P作用在跨中C点时如图6(b),其弯矩图如图6(c)所示,C截面的弯矩是全梁的绝对最大弯矩 M  =M =M =5P/4=1.25P(1) =5P/4=1.25P(1)设工字钢的惯性矩为I  ,抗弯截面系数为W ,抗弯截面系数为W ,而中间加强部分截面的惯性矩和抗弯截面系数为I′ ,而中间加强部分截面的惯性矩和抗弯截面系数为I′ 、W′ 、W′ 。查型钢表 。查型钢表I  =2370×10 =2370×10 m m ,W ,W =237×10 =237×10 m m I′  =2370×10 =2370×10 +2×(10×120×105 +2×(10×120×105 ×10 ×10 )=5020×10 )=5020×10 8m 8m 这里钢板对其自身形心轴的惯性矩很小,已略去。 W′  =I′ =I′ /y′ /y′ =5020×10 =5020×10 /110×10 /110×10 =456×10 =456×10 m m 由正应力强度条件得 M  ≤W′ ≤W′ [σ]=456×10 [σ]=456×10 ×152×10 ×152×10 =69.3×10 =69.3×10 N·m=69.3kN·m(2) N·m=69.3kN·m(2)由式(1)、式(2)两式得容许荷载 [P]  =4M =4M /5=4/5×69.3=55.4kN(3) /5=4/5×69.3=55.4kN(3)2.荷载作用在D点时,由D截面的正应力强度求[P]。 当荷载P作用在D点时(图6d),其弯矩图如图6(e)。 M  =1.008P(4) =1.008P(4)由正应力强度条件得 M  ≤W ≤W [σ]=237×10 [σ]=237×10 ×152×10 ×152×10 =36.0×10 =36.0×10 N·m=36.0kN·m(5) N·m=36.0kN·m(5)由式(4)、式(5)两式得[P]  =M =M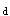 /1.008=36.0/1.008=35.77kN(6) /1.008=36.0/1.008=35.77kN(6)3.当荷载趋近A截面时,由A右截面的剪应力强度求[P]。 此时Q 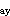 =Q =Q ≈P(7) ≈P(7)查型钢表I  /S /S =17.2cm,d=7mm,由剪应力强度条件得 =17.2cm,d=7mm,由剪应力强度条件得Q  ≤I ≤I d[t]/S d[t]/S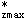 =17.2×10 =17.2×10 ×7×10 ×7×10 ×95×10 ×95×10 =114×10 =114×10 N=114kN(8) N=114kN(8)由式(7)、式(8)得 [P]  =Q =Q =114kN(9) =114kN(9)比较式(3)、式(6)、式(9)得 [P]=35.7kN 所以答案A是正确的。答案B的错误是误认为[P]是由P力作用在C截面时,由C截面的正应力强度决定的;答案C的错误是误认为[P]是由剪应力强度决定的;而答案D的错误是误认为[P]是当P力作用在C截面时,由D截面的正应力强度决定的。 |
|
|
2.用叠加法求图7悬臂梁自由端B的转角θ 和挠度f 和挠度f 为( )。 为( )。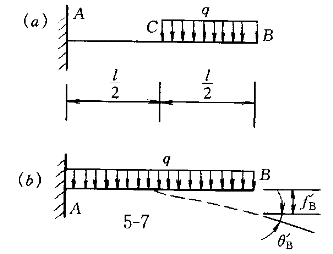 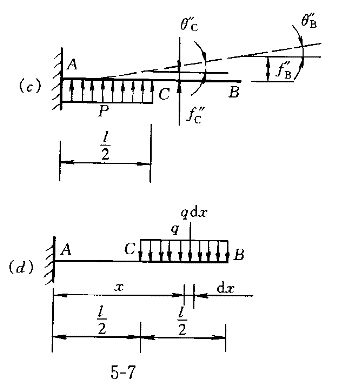 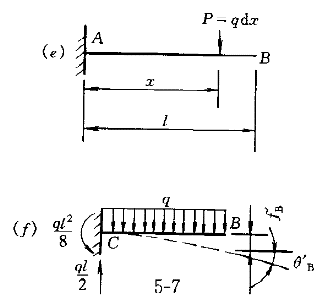 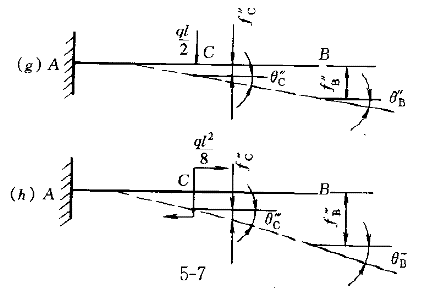 |
| 正确答案:D 解题思路:解:弯曲变形部分多考叠加法求梁的变形,因为叠加法可以利用已有表格,很快求出,工程上应用很广。但叠加法有多种:(1)荷载分解,变形叠加;(2)求梁不变形部分上的位移的叠加法;(3)逐段刚化法。这里结合本例阐明上述三种叠加法。 解法一 将图7(a)所示荷载分解为图7(b)和图7(c)所示两种荷载的叠加,即第一种叠加法,但在计算图7(b)所示荷载的梁CB部分的位移需用到第二种叠加法。对于图7(b)所示情况, 由表可查得 θ′  =ql =ql /6EI,f′ /6EI,f′ =ql =ql /8EI /8EI对于图7(c)所示情况,可查得 θ″  =-q(l/2) =-q(l/2) /6EI=-ql /6EI=-ql /48EI,f″ /48EI,f″ =-q(l/2) =-q(l/2) /8EI=-ql /8EI=-ql /128EI /128EI由于BC段弯矩为零,变形后仍为直线,由第二种叠加法得 θ″  =θ″ =θ″ =-q(l/2) =-q(l/2) /48EI,f″ /48EI,f″ =f″ =f″ l/2=-7(l/2) l/2=-7(l/2) /384EI /384EI叠加后得出 θ  =θ′ =θ′ +θ″ +θ″ =ql =ql /6EI-ql /6EI-ql /48EI=7ql /48EI=7ql /48EIf /48EIf =f′ =f′ +f″ +f″ =ql =ql /8EI-ql /8EI-ql /384EI=41ql /384EI=41ql /384EI /384EI所以,答案D是正确的。 解法二 将实际荷载看做是由无穷多个微小集中力叠加而成(图7d),距左端为x处的微小集中力qdx所产生的变形可根据图7(e)查表,它所引起的B截面的挠度和转角分别记作df  和dθ 和dθ ,其值为 ,其值为dθ  =(qdx)x =(qdx)x /2EIdf /2EIdf =(qdx)x =(qdx)x (3l-x)/6EI (3l-x)/6EI叠加即将上两式从l/2到l区间积分,得出 θ  =JZ105_112_7_1.gifqx =JZ105_112_7_1.gifqx dx/2EI=7ql dx/2EI=7ql 48EI 48EIf  = =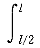 qx qx (3l-x)dx/6EI=41ql (3l-x)dx/6EI=41ql /384EI /384EI与解法一结果相同。 解法三 运用第三种叠加法即逐段刚化法,将图7(a)分解为图7(f)、(g)、(h)三种情形叠加。对于图7(f)所示情况,查表得 θ′  =q(l/2) =q(l/2) /6EI=ql /6EI=ql /48EI,f′ /48EI,f′ =4(l/2) =4(l/2) /8EI=ql /8EI=ql /128EI /128EI对于图7(g),查表有 θ″  =(ql/2)(l/2) =(ql/2)(l/2) /2EI=ql /2EI=ql /16EI,f″ /16EI,f″ =(ql/2)(l/2) =(ql/2)(l/2) /3EI=ql /3EI=ql /48EI /48EI从而有 θ″  =θ″ =θ″ =ql =ql /16EI,f″ /16EI,f″ =f″ =f″ +θ″ +θ″ l/2=5ql l/2=5ql /96EI /96EI对于图7(h),查表得 θ   =ql =ql /8(l/2)/EI=ql /8(l/2)/EI=ql /16EI,f /16EI,f  =ql =ql.gif) /8(l/2)/EI=ql /8(l/2)/EI=ql /64EI /64EI故有 θ   =θ =θ  =ql =ql /16EI,f /16EI,f  =f =f  +q +q  l/2=ql l/2=ql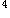 /64EI /64EI三者叠加,得 θ  =θ′ =θ′ +θ″ +θ″ +θ +θ  =7ql =7ql /48EI /48EIf  =f′ =f′ +f″ +f″ +f +f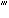  =41ql =41ql /384EI /384EI结果与前两种解法相同。在三种解法中,以解法二最简便。 答案A中θ  的错误是因图7(c)中θ″ 的错误是因图7(c)中θ″ 的符号搞错所致。f 的符号搞错所致。f 的错误是θ″ 的错误是θ″ 的符号搞错引起的;答案B的错误是因图7(g)中未计入θ″ 的符号搞错引起的;答案B的错误是因图7(g)中未计入θ″ 和θ″ 和θ″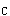 引起的;答案C的错误是未计入图7(h)中的θ″ 引起的;答案C的错误是未计入图7(h)中的θ″ 和f″ 和f″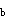 引起的。 引起的。 |
|
|
3.图8(a)所示三向应力状态,其最大剪应力为( )。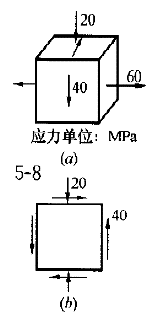 |
正确答案:D 解题思路:解:图示单元体的一对平面是主平面,其主应力σ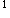 =60MPa。因为平行于主应力σ′的面内主应力与σ′无关。此时,可以应用叠加原理,将该单元体简化为二向应力状态与单向应力状态叠加。 =60MPa。因为平行于主应力σ′的面内主应力与σ′无关。此时,可以应用叠加原理,将该单元体简化为二向应力状态与单向应力状态叠加。不考虑σ′的二向应力状态如图8(b)所示。该二向应力状态的主应力为 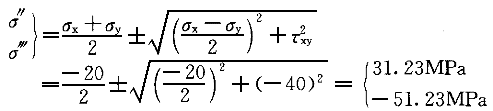 考虑到σ′=60MPa,按σ  >σ >σ >σ >σ 关系,单元体的主应力为 关系,单元体的主应力为σ  =60MPaσ =60MPaσ =31.23MPaσ =31.23MPaσ =-51.23MPa =-51.23MPa单元体的最大剪应力 τ 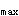 =σ =σ -σ -σ /3=60-(-51.23)/2=55.6MPa /3=60-(-51.23)/2=55.6MPa所以D的答案正确。若未考虑σ′=60MPa的影响,就得A的错误答案。若未考虑σ  >σ >σ >σ >σ 关系,就得 B的错误答案。若未考虑σ 关系,就得 B的错误答案。若未考虑σ ,σ ,σ 的影响,就得出C的错误答案。 的影响,就得出C的错误答案。 |
|
|
4.一钢制圆轴受拉、扭组合荷载作用如图9(a)所示,已知圆轴直径d=20mm,材料弹性模量E=200GPa。如果采用直角应变花在测定轴表面O点的应变值:ε90°=96×10 ,ε45°=565×10 ,ε45°=565×10 ,ε0°=320×10 ,ε0°=320×10 ,则转矩M ,则转矩M 为( )。 为( )。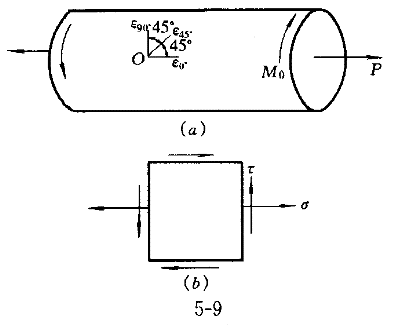 |
正确答案:D 解题思路:解:1.轴表面上的应力状态如图9(b)所示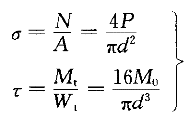 2.求横截面上的正应力 σ=Eε0°=200×10 .gif) ×320×10 ×320×10 =64×10 =64×10 Pa=64MPa(2) Pa=64MPa(2)3.求横向变形系数 v=|ε90°/ε0°|=|-96×10  /32×10 /32×10 |=0.3 |=0.34.由广义虎克定律求剪应力τ 先由斜截面上应力公式求σ45°,σ-45°。 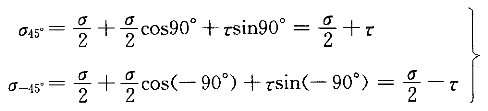 由广义虎克定律,有 ε45°=1/E(σ45°-vσ-45°)=1/E[(σ/2+τ)-v(σ/τ)]=1/E[(v)σ/2+(1+v)τ](4)σ 由前已求得,ε45°已知,由此可求得 τ= 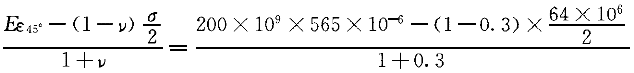 =69.7×10 =69.7×10 Pa=69.7MPa Pa=69.7MPa5.求外力偶矩M  由式(1)得 由式(1)得M .gif) =πd[ =πd[ τ/16=π×20 τ/16=π×20.gif) ×10 ×10 /16×69.7×10 /16×69.7×10 =109.4N·m =109.4N·m所以,答案D是正确的。 若将横向变形系数误计为v=|ε0°/ε90°|=3.33,得A的错误答案,实际上v<0.5;若不将v取绝对值,即误认为v=-0.3,就得出B的错误答案;若不考虑轴向正应力ε对ε45°的影响,就得到C的错误答案。 注意,平面应力状态的广义虎克定律只要两正应力相互垂直即可应用。 |
|
|
5.已知轴的转速n=183.5r/min,材料为45号钢,G=80GPa.[τ]=40MPa,[θ]=1.5°/m,三个齿轮的输入,输出功率分别为N =3.736kW,N =3.736kW,N =0.756kW,N =0.756kW,N =2.98kW。此轴的最合理的直径为: =2.98kW。此轴的最合理的直径为: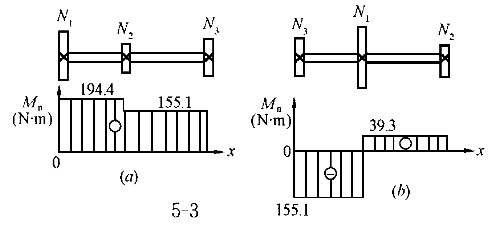 |
| 正确答案:C 解题思路:解:1.计算外力偶矩 m  =9549N =9549N.gif) /n=9549(3.736/183.5)=194.4N·m /n=9549(3.736/183.5)=194.4N·mm .gif) =9549(0.756/183.5)=39.3N·m =9549(0.756/183.5)=39.3N·mm .gif) =9549(2.98/183.5)=151.1N·m =9549(2.98/183.5)=151.1N·m2.截面设计若按图3(a)布置齿轮,轴的最大扭矩M  =194.4N·m,按强度条件设计,得 =194.4N·m,按强度条件设计,得d≥ 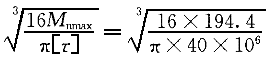 =29×10 =29×10 m=29mm m=29mm按刚度条件设计,得 d≥ 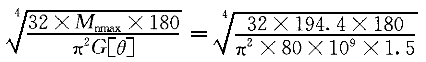 =31×10 =31×10 m=31mm m=31mm所以应取d=31mm,这便是D的结果。虽说满足强度条件和刚度条件,但设计是否合理呢?下面再来看看另一种齿轮布置方案。 若按图3(b)布置齿轮,最大扭矩的绝对值为|M 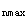 |=155.1N·m按强度条件设计,得: |=155.1N·m按强度条件设计,得:d≥ 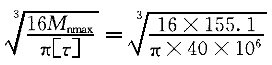 =27×10 =27×10 m=27mm m=27mm按刚度条件设计,得 d≥ 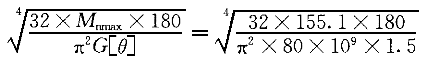 =29.5×10 =29.5×10 m=29.5mm m=29.5mm所以,最佳方案是按图3(b)配置齿轮,合理轴径为d=30mm,故应选择C的结果。A的结果不满足刚度条件,B的结果也不满足图3(6)方案的刚度条件,D的结果不合理。 |
- 2012年岩土工程师考试基础知识模拟试题:工程地质(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:理论力学(单项选择题1)
- 2012年岩土工程师考试基础知识模拟试题:高等数学(单项选择题3)
- 2012年岩土工程师考试专业知识考前冲刺(五)上午卷
- 2016年岩土工程师考试《综合知识》冲刺练习(4)
- 2012年岩土工程师考试基础知识模拟试题:弹性力学和结构力学(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(3)
- 2012年岩土工程师考试基础知识模拟试题:电工与电子技术(单项选择题2)
- 土工结构、边坡与支挡结构、基坑与地下工程(单项选择题2)
- 2016年岩土工程师考试《综合知识》冲刺练习(5)

